링크드리스트에는 단일, 양방향, 원형 등이 있다. 해당 글에서는 양방향 링크드 리스트를 알아보자. 먼저 링크드 리스트란 논리적인 개념으로 포인터를 활용하여 메모리 순차적인 공간에 data를 만드는 것이다. 얼핏 느끼기엔 배열과 비슷하다. 배열 역시 메모리의 순차적인 공간에 특정 data들이 나열되어 있기 때문이다. 배열과 차이점은 무엇일까?
배열과 차이점
배열은 아래와 같이 선언하게 되어있다. 물론 이것은 모두가 아는 내용.
int Arr[4];메모리 구조적으로 보면 배열은 컴파일타임에 메모리에 공간이 할당된다. 그렇다. 즉, stack 혹은 data 영역에 메모리가 할당 된다는 뜻이다. (stack과 data 메모리 구조가 기억이 나지 않는다면 아래 글을 보자.)
2021.09.03 - [SW/C] - [메모리구조] 프로그램의 메모리구조, Text, Data, Heap, Stack
[메모리구조] 프로그램의 메모리구조, Text, Data, Heap, Stack
우리가 프로그램을 작성하여 실행시키면 OS에 의해 메모리 공간이 할당된다. 바로 RAM영역이다. 할당된 영역은 크게 3가지로 나뉜다. 아래 그림을 보자. Text 영역 : 문자열상수등이 저장된다. Data
gangdor.tistory.com
그러나 링크드리스트는 배열과 달리 동적할당을 통해 노드를 생성한다. 즉 heap영역의 메모리 공간에 할당되게 된다.
링크드리스트의 이점
간단명료한 배열과 달리 링크드리스트는 구현이 필요하기는 하나 데이터 노드의 편입, 삭제 등이 용이하다. 배열의 경우 연속된 index사이에 값을 추가하거나 삭제하려면 공간을 마련하고 삭제하기 위해 각 data들을 앞으로 당기고 뒤로 밀고 해야한다. 시간 복잡도가 매우 높다. 그러나 링크드 리스트를 활용하면 노드의 연결고리만 잘 지정해주면 되므로 배열보다 훨씬 용이하다. 양방향 링크드리스트는 아래의 그림과 같다.

Head와 Tail을 하나의 노드라고 생각하면 각 노드가 서로를 가리키게 만드는 것이다. 따라서 그림과 같이 하나의 노드에는 data, prev, next가 필요하다. 각각 노드가 가지고 있는 data값, 이전 노드의 주소, 다음 노드의 주소가 되겠다. 코드로 표현하면
struct Node{
int data;
struct Node* prev;
struct Node* next;
}typedef Node;이와 같겠다. 특정 data를 가지는 변수와 자기참조 구조체 포인터를 활용하여 이전 이후 노드의 주소를 담고 있어야한다. 위의 그림을 보면 Head와 Tail이 있는데 이는 링크드 리스트의 시작과 끝을 나타낸다. 노드는 이 두 시작과 끝 노드의 사이에 존재하게 된다. 따라서 Head와 Tail에는 따로 data를 싣지 않는 것이 편리하다. cur포인터는 Tail을 가리키게되는데 노드의 삽입과 삭제에 사용된다. cur를 통해 하는 동작은 크게 4가지이다. 노드의 삽입, 노드의 삭제, 순회에 필요한 cur 좌측이동, 우측이동이다.
노드의 삽입
노드의 삽입을 알아보자. 양방향 연결리스트 초기 상태에서 cur를 이용하여 노드를 삽입한다. 아래 그림처럼 되는 것을 예상할 수 있다. 코드를 보면서 이해해보자.

void Insert(int data)
{
Node* new_node = (Node*)malloc(sizeof(Node)); //Insert를 위해 노드 메모리 동적할당
new_node->data = data; //새로운 노드의 data 초기화
new_node->next = cur; //새 노드의 next 값은 cur로 설정
new_node->prev = cur->prev; //새 노드의 prev값은 cur의 prev로 설정
cur->prev->next = new_node; //cur의 바로 앞 노드를 new node 가리키게 하기
cur->prev = new_node; //cur의 이전 노드 주소를 new node가리키게 하기
}먼저 새로운 노드를 삽입해야하므로 새로운 Node를 만들자. malloc을 활용하여 동적할당으로 Node를 만들 수 있다. 이후 새로운 노드를 먼저 setting해준다고 생각하자. data를 넣고 리스트 사이로 양팔을 벌리는 것이다. 아래 그림처럼.

이후 기존에 cur과 바로 앞 노드가 서로 가리켰던 pointer를 새로 삽입하려는 Node의 주소로 지정해주면 되곘다. 아래 그림을 참조하자.

사실 어느정도 이해가 필요하고 암기가 되어야하는 부분인데 양팔을 벌릴때 왼쪽부터 팔을 벌린다고 생각하면 순서를 기어하기 쉬울 것이라 생각한다. 즉, cur의 앞쪽 노드부터 처리하는 것이다. cur->prev값을 먼저 바꿔버리면 cur의 앞 노드 주소를 기억하는 변수가 없기 때문이다. 삽입노드를 만들때는 양팔을 벌리되, 왼쪽 먼저!
노드의 삭제
노드의 삭제를 이해해보자. 앞 그림에 추가했던 노드를 삭제할 것이다. 코드를 보며 이해해보자.
void Delete(){
if(cur->prev != head) //cur의 앞노드가 head이면 추가된 노드가 없으므로 삭제를 하면 안된다.
{
cur->prev = cur->prev->prev; //왼쪽으로 향한다.cur->prev를 이전 노드의 이전 노드로 가리킨다.
free(cur->prev->next); //cur->prev는 이전이전노드이나 이전이전노드의 다음노드를 먼저 해제
cur->prev->next = cur; //해제 후 이전노드의 다음노드를 cur로 설정
}
}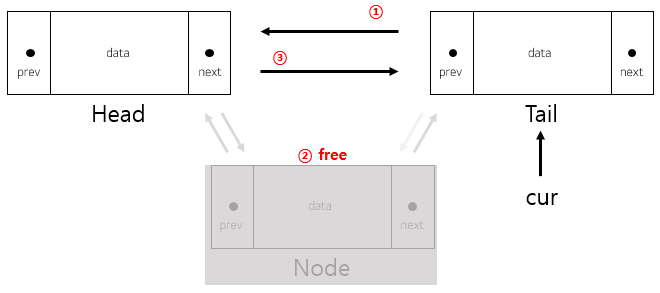
마찬가지로 왼쪽부터 작업을 해주어야 한다. 왼쪽이라함을cur->prev를 가리킨다. 해당주소를 이전노드의 이전노드로 지정한다. 이후 할당된 메모리를 free() 해준다. 삭제 후 이전노드의 다음 노드를 cur로 지정해주면 되겠다. 역시 왼쪽부터!
탐색커서 좌우측 이동
탐색커서는 비교적 간단하다. 코드를 보면 바로 이해가 갈 것이다.
void Left()
{
if(cur->prev != head) //cur->prev가 head면 삭제할 노드가 없으므로 head를 삭제하면 안된다.
{
cur= cur->prve; //cur의 주소값을 cur->prev로 이동한다.
}
}
void Right()
{
if(cur != tail) //cur가 tail이면 더이상 커서를 이동할 수 없다.
{
cur= cur->next; //cur의 주소값을 cur->next로 이동한다.
}
}주의할 것은 cur의 이동이 head와 tail의 범주 안에서 가능해야 한다는 것이다. cur의 이동으로 값을 탐색하고 리스트를 순회할 수 있으므로 알아두도록 하자.
리스트 구현에 필요한 삽입 및 삭제, 이동을 알아보았으니 이를 활용한 링크드리스트 문제의 전체 코드를 보며 마무리를 해보자. head와 tail의 초기화 작업정도만 유의해 보면 될 것이다.
#include <stdio.h>
#include <stdlib.h>
char S[100000+100];
char C[500000+100];
char str[600000+100];
//양방향 linkedlist
struct Node{
char data;
struct Node* prev;
struct Node* next;
}typedef Node;
Node* head;
Node* tail;
Node* cur;
void Input(){
scanf("%s", S);
scanf("%s", C);
}
void Insert(char d){
Node* p = (Node*)malloc(sizeof(Node));
p->data = d;
p->prev = cur->prev;
p->next = cur;
cur->prev->next = p;
cur->prev = p;
}
void Left()
{
if(cur->prev != head)
cur=cur->prev;
}
void Right()
{
if(cur!=tail)
cur=cur->next;
}
void Delete()
{
if(cur->prev != head)
{
cur->prev = cur->prev->prev;
free(cur->prev->next);
cur->prev->next = cur;
}
}
void Solve(){
//링크드리스트 준비 HEAD, TAIL, CUR
head = (Node*)malloc(sizeof(Node));
cur = tail = (Node*)malloc(sizeof(Node));
head->next = tail;
tail->prev = head;
tail->next = NULL;
//Insert
int i=0;
while(S[i]!='\0')
{
Insert(S[i]);
i++;
}
i=0;
while(C[i]!='\0')
{
switch(C[i])
{
case 'L':
Left();
break;
case 'R':
Right();
break;
case 'B':
Delete();
break;
default :
Insert(C[i]);
break;
}
i++;
}
Node* temp;
temp = head->next;
i=0;
while(temp!=tail)
{
str[i]=temp->data;
temp=temp->next;
i++;
}
}
int main() {
Input();
Solve();
printf("%s",str);
return 0;
}'SW > Algorithm' 카테고리의 다른 글
| 지렁이게임, 문제 해결 훈련 (1) | 2021.09.07 |
|---|---|
| 투자게임, 문제해결 훈련, 역방향 탐색 (0) | 2021.09.07 |
| DFS, 순열구하기, 조합구하기 (0) | 2021.09.01 |
| 아이템먹기, 원형 큐 사용하기 훈련 (0) | 2021.08.31 |
| [이진탐색] Binary Search, lower-bound, upper-bound (0) | 2021.08.24 |