순열은 조합과는 다르다. 순열은 순서가 중요시 되는 수열이다.
예를들어 5개의 숫자 중 3개를 순서에 상관없이 고르는 것은 조합이다.
즉, 조합에서 (1,2,3)과 (3,2,1)는 같은 경우로 판단된다.
그러나 순열은 다르다. 순서가 중요하기 때문에 순열에서 (1,2,3)과 (3,2,1)은 다르다.

중고등학교에서 배웠던 공식이 기억날 것이다. 사실 기억나지 않는다. 0!은 1이다. 기억을 더듬어 5개의 숫자중에 3가지를 뽑아내는 조합의 경우의 수는 10이며, 순열은 60가지가 되겠다. 이를 코드로 어떻게 구현할 수 있을까?
순열
보통의 경우 DFS 알고리즘으로 순열을 구현할 수 있다. 5가지의 수 중에 3가지를 뽑아내는 순열의 경우는 아래와 같다.
void Dfs_permutation(int level){
if(level>3){
//성공 및 종료
for(int i=1; i<=3; i++)
printf("%d ",seq[i]);
printf("\n");
total++;
return;
}
//확산
for(int i=1; i<=5; i++){ //순서가 중요하므로, 재귀를 하더라도 i를 1부터 시작하여 선택했던 숫자도 다시 살핀다.
if(used[i] == 1) continue;
used[i]=1;
seq[level]=i;
Dfs_permutation(level+1);
used[i]=0;
}
}
파라미터 지정
순열에서 파라미터는 선택하는 level을 지정해주었다. 숫자를 선택하는 단계라고 이해하면 되겠다. 알고리즘 문제에서 파라미터는 자율적으로 설정할 수 있다.
종료조건
DFS는 기본적으로 재귀함수이기 때문에 함수를 종료할 수 있는 적절한 종료조건이 필요하다. 종료조건이 없다면 무한으로 함수가 호출되어 프로그램이 불능에 빠질 수 있다. 적절한 종료조건으로 여기서는 3개보다 많이 선택하려고 할 시, 종료할 수 있게 설정하였다.
확산
이후 for문을 통해 DFS 확산을 할 수 있는데 이 때문에 DFS가 디버깅하기 참으로 까다로운 부분이다. 우선 i는 선택하는 숫자라고 생각하자. 순자는 1부터 5까지 선택할 수 있게 된다. 여기서 이미 숫자를 선택했다면 continue를 통해 해당 숫자의 추가 작업을 수행하지 않는다.
선택표시, True
visit 혹은 check 배열을 통해 선택된 숫자를 표시한다. 이후 DFS를 level을 올려서 진행하게 되는 것이다. DFS는 깊이 우선 탐색이니 만큼 이전 level의 for문을 다 수행하지 않고 다음 level로 재귀함수 호출에 의해 넘어가게 된다.
결국 DFS는 level이 증가하여 종료조건에 다다를때까지 호출되게 된다.
선택표시, False
이후 호출된 해당 함수가 return에 의해 종료되면, 이전 레벨로 돌아가 마저 수행하지 못한 for문을 수행하게 된다. 여기서는 DFS(level+1)이후를 수행할테니 visit[i]=0을 수행하겠다. 왜 visit[i]=0을 다시 되돌리는 것일까? 여기서 우리는 BackTracking의 개념을 알아야하는데 쉽게 말해서 앞 level에서 선택했던 숫자를 다시 선택하지 않은 것으로 되돌리는 것이다. 그래야 다른 조합구성도 가능하지 않겠는가?
이를 노드로 표현하면 아래와 같이 표현할 수 있다.

여기까지가 순열의 구현이되겠다. 중요한 패턴이므로 익숙해지도록 하자.
다음은 조합이다.
조합
조합은 순열과 구현부가 매우 흡사하지만, 파라미터가 다르다. 순열과 조합의 차이점은 순서를 중요하게 여기느냐 여기지 않느냐의 차이다. 순열에서는 순서가 중요하기때문에 방문했던 노드라도 다시 탐색할 필요가 있었다. 때문에 확산 시에 for문의 Index를 1부터 순차적으로 설정해 주었다. 조합에서는 순서가 중요하지 않다. 따라서 이미 선택한 숫자를 다시 확인할 필요가 없는 것이다. 따라서 파라미터로 시작 노드의 idx를 알리는 것이 필요하다. 아래의 코드를 보자.
void Dfs_combination(int idx, int level){
if(level > 3){
for(int i=1; i<=3; i++)
printf("%d ",seq[i]);
printf("\n");
total++;
return;
}
for(int i=idx; i<=5; i++){
if(used[i]) continue;
used[i]=1;
seq[level]=i;
Dfs_combination(i,level+1);
used[i]=0;
}
}종료조건, 선택여부 표시의 백트래킹 모두 순열과 같다. 다만, 파라미터와 이를 활용한 확산부가 다르다.
파라미터
파라미터는 level은 동일하게 가져가면서 조합에서는 idx라는 시작 인덱스 위치가 필요하다. 시작 인덱스는 이미 선택한 숫자에 대해서는 탐색하지 않기 위해 사용된다.
확산
넘겨받은 idx를 확산부에서 iterator의 시작으로 설정하였다. 즉, i는 파라미터인 idx부터 출발한다. 이것이 무슨 차이가 있는 걸까? 아래의 그림을 보자. 아래그림은 4개의 숫자중 3개를 조합하는 경우이다.
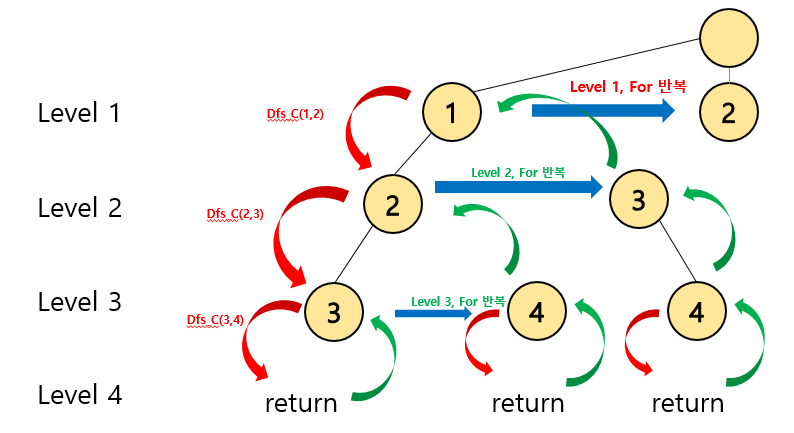
확산시에 idx파라미터부터 시작하기 때문에 이전에 선택된 노드는 더이상 확인하지 않는다. 재귀함수 호출시에 idx값을 전달하게 된다. 가령 (1,2,3)으로 조합을 마친 후, return하면 i=3이므로 우리는 선택표시 해제를 하게 된다. i가 4까지 확산을 마치게 되고 level2 까지 return하게 된다. 이때의 used는 1뿐이다. Level 2의 아직 다 수행되지 않은 for문 반복을 통해 i는 3으로 증가하게 되고 확산을 지속한다. BackTracking은 동일하기 때문에 level3 확산 후에 선택하는 인덱스 i가 1부터 시작했다면 (1,3,2)가 선택 되었을 것이다.
※ i=2일때 for반복을 종료하며 BackTracking 초기화를 했기때문에.
그러나 idx를 level3에 파라미터로 넘겼기 때문에 level3의 for문은 i=3부터 시작된다. 따라서 (1,3,4)가 조합되는 것이다.
글로는 설명이 굉장히 복잡할 수 있다. 코드를 보며 손으로 노드를 그려가며 따라가는 것이 이해에 도움을 줄 수 있다.
조합 및 순열의 전체코드는 아래와 같다.
#include <stdio.h>
int used[10+100];
int seq[10+100];
int total;
void Dfs_permutation(int level){
if(level>3){
//성공 및 종료
for(int i=1; i<=3; i++)
printf("%d ",seq[i]);
printf("\n");
total++;
return;
}
//확산
for(int i=1; i<=5; i++){ //순서가 중요하므로, 재귀를 하더라도 i를 1부터 시작하여 선택했던 숫자도 다시 살핀다.
if(used[i] == 1) continue;
used[i]=1;
seq[level]=i;
Dfs_permutation(level+1);
used[i]=0;
}
}
void Dfs_combination(int idx, int level){
if(level > 3){
for(int i=1; i<=3; i++)
printf("%d ",seq[i]);
printf("\n");
total++;
return;
}
for(int i=idx; i<=5; i++){
if(used[i]) continue;
used[i]=1;
seq[level]=i;
Dfs_combination(i,level+1);
used[i]=0;
}
}
int main() {
//Dfs_permutation(1);
//printf("Permutaion total : %d",total);
Dfs_combination(1,1); //시작하는 숫자, level
printf("Combination total : %d",total);
return 0;
}
'SW > Algorithm' 카테고리의 다른 글
| 투자게임, 문제해결 훈련, 역방향 탐색 (0) | 2021.09.07 |
|---|---|
| [양방향 연결리스트] 양방향 링크드리스트, Linked List 개념 (0) | 2021.09.06 |
| 아이템먹기, 원형 큐 사용하기 훈련 (0) | 2021.08.31 |
| [이진탐색] Binary Search, lower-bound, upper-bound (0) | 2021.08.24 |
| [이진탐색] 작품상 투표 (0) | 2021.08.23 |